Daze

  用 jmuOutlier::rlaplace(250*100000,0.0002,0.0125) 取代 rnorm(250*100000,0.0002,0.0125) Daily return的density: 1xETF median  3.08%，mean  5.17%，SD 21.02%，geomean  3.13% 2xETF median  2.22%，mean 10.61%，SD 45.53%，geomean  2.26% 3xETF median -2.45%，mean 16.36%，SD 75.44%，geomean -2.51%

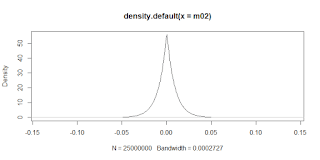
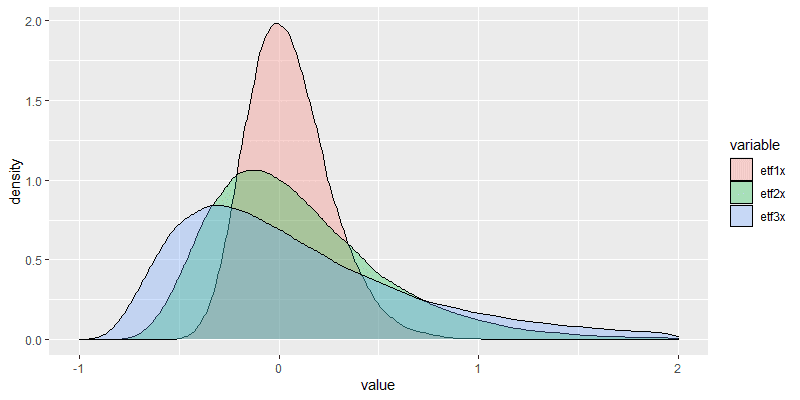
require(matrixStats) require(tidyr) require(ggplot2) m02 <- matrix( rnorm(250*100000, 0.0002, 0.0125), ncol = 250 ) dfprod <- matrix(0,nrow=100000,ncol = 5) %>% as.data.frame colnames(dfprod) <- c("etf1x","etf2x","etf3x","etf2x_cost","etf3x_cost") dfprod$etf1x <- (m02 + 1) %>% rowProds dfprod$etf2x <- (m02*2 + 1) %>% rowProds dfprod$etf3x <- (m02*3 + 1) %>% rowProds dfprod$etf2x_cost <- (m02*2 + 1 - 0.00006) %>% rowProds dfprod$etf3x_cost <- (m02*3 + 1 - 0.00008) %>% rowProds long_prod <- gather(dfprod) long_prod$value <- long_prod$value-1 ggplot(long_prod, aes(x=value, fill=key)) + geom_density(alpha=.3)+xlim(-1,2) median(dfprod$etf1x) mean(dfprod$etf1x) sd(dfprod$etf1x) exp(mean(log(dfprod$etf1x)))

假設Daily return滿足normal distribution。 令Daily return=2bp，Daily SD= 125bp。 (每年約250交易日，約當年報酬率5%，年標準差20%) 生成100000筆250日的日回報率。 在不考慮ETF cost 的狀況下，250個交易日後，1x、2x、3xETF的回報率: 1xETF median 3.15%，mean 5.11%，SD 21.00% 2xETF median 2.33%，mean 10.48%，SD 45.44% 3xETF median -2.41%，mean 16.13%，SD 75.38% 加入cost (1xETF daily cost = 0, 2xETF daily cost=0.6bp, 3xETF daily cost=0.8bp，約當ER 1%，借貸成本 0.5%): 1xETF median 3.15%，mean 5.11%，SD 21.00% 2xETF median 0.81%，mean 8.84%，SD 44.77% 3xETF median -4.34%，mean 13.83%，SD 73.90% 不考慮cost，比較50%  1xETF + 50% 3xETF不再平衡 vs 100% 2xETF: 2xETF median 2.33%，mean 10.48%，SD 45.44% 50%  1xETF + 50% 3xETF不再平衡   median 0.37%， mean 10.62%，SD 47.85% 加入cost   (1xETF daily cost = 0, 2xETF daily cost=0.6bp, 3xETF daily cost=0.8bp)， 比較50%  1xETF + 50% 3xETF不再平衡 vs 100% 2xETF: 2xETF median 0.81%， mean 8.84%，SD 44.77% 50%  1xETF + 50% 3xETF不再平衡  median -0.59%，mean 9.47%，SD 47.11% Margin loan 1倍投入1xETF vs 2xETF (不考慮強制平倉): 註: 各張圖的value 大於2的部分被刻意切掉了，否則0附近太擠了 註2: R code 註3: If considering

假設有一家保險公司能夠精準計算你的各項風險並承保。但是在精算出你的風險保費之後，要乘上一定的倍率收取保費。你應該保多少額度呢? 假設效用函數滿足Constant Relative Risk Aversion，且事件發生率不太大，理想的「不」保險額度約等於 1 - x^(-1/y)，其中 x 是收費倍率，y是 相對風險趨避係數(RRA) 。 (註1) 舉例來說，一個RRA=2的人，在倍率=1.3的狀況下，理想的「不」保險額度約等於12.29%。這個百分比是相對於總資產 (註2) 的額度。如果總資產有1000萬元，有一個事件的可能損害是300萬元，則應該為這個事件投保300萬-1000萬*12.29%=177.1萬的保險額度。事件可能損害如果低於122.9萬的話則應選擇完全不投保。 上面有提到，「事件發生率不太大的話」。理想的「不」保險額度會隨事件發生率提高而提高，隨可能損害降低而提高。不過以發生率10%來說，理想的「不」保險額度最多從12.29%上升到13.76%左右。 以汽車第三人責任險來說，如果能只保超額險的部分可能就比較理想了。可惜保險公司很少讓人稱心如意。 註1: 如果對計算過程有興趣，可參見 此 。 註2: 未來收入是否應折現計入總資產看個人觀點。我個人認為應該計入。

  x= 收費倍率 y=RRA z= 損害 w= 不保險額度 u= 事件發生率 效用函數 U(x,y,z,w,u)=( (1-w-(z-w)*u*x)^(1-y)-1)/(1-y)*u + ( (1 -(z-w)*u*x)^(1-y)-1)/(1-y)*(1-u) ∂U/∂w =  ((1 - u) u x)/(1 - u x (-w + z))^y + (u (-1 + u x))/(1 - w - u x (-w + z))^y If u is small enough,  ((1 - u) u x)/(1 - u x (-w + z))^y + (u (-1 + u x))/(1 - w - u x (-w + z))^y   ≈  u*(x- 1/(1-w)^y) u*(x- 1/(1-w)^y) = 0   =>   w = 1-x^(-1/y)

「風險自留」在保險上是個重要的觀念。對於低損害的事件，沒有保險的必要，可以自行承擔損失。那麼，什麼程度的損害才算夠低，而適合風險自留呢?在此試著透過 效用函數 的觀點提出一種解答。(假設效用函數滿足Constant Relative Risk Aversion) 假設有一家保險公司能夠精準計算你的各項風險並承保。但是保險公司畢竟不是慈善事業，在精算出你的風險保費之後，要乘上130%收取保費。哪些風險應該保險而哪些保險應該自留呢? 這個問題的答案，當然要看你對風險的趨避程度。越是不喜歡風險，即使較低的損害也可能有保險的必要。 上表的意義是，在130%保費下，如果相對風險趨避係數(RRA)為1，事件的損害等於總資產(註1)的45%，則當事件發生率小於7.28%時，保險的期望效用高於不保險的期望效用，應該保險。(註2) 但是，很容易注意到，上表有很多格子都是0。這些為0的格子，代表不管事件的發生率是多少，保險的期望效用都低於不保險的期望效用，應該不保險。 在130%保費下，如果你的RRA是1，總資產40%以下的損害應該不保險。RRA是2，總資產20%以下的損害應該不保險。RRA是3，總資產15%以下的損害應該不保險。 不過，上表是在完全保險與不保險之間做比較。如果允許只保一半呢? (理賠減半，保費也減半) 可以看到，為0的格子數減少了。 如果允許只保0.1倍風險的話，RRA=1在Damage= -0.25仍然有解。至於只保0.1倍風險是否實用另當別論。不過似乎找不到保險倍率能讓RRA=1在Damage= -0.2有解。(沒有解的Damage，RRA=1似乎是落在-0.23左右，RRA=2約-0.12，RRA=3約-0.08，RRA=4約-0.06。) 註1:我會建議將未來人力資本折現計入總資產。但也許有些人比較喜歡用現有總資產來計算。 註2:  如果想自行驗算表中數字，方程式是 ln( 1 + Damage)*x = ln(1 + Damage*x*1.3) ; if RRA=1 (1-(1+Damage)^(1-RRA))/(1-RRA)*x = (1 - (1+Damage*x*1.3)^(1-RRA))/(1-RRA) ; if RRA≠1 只保一半的方程式是 ln( 1 + Damage)*x = ln(1 + Damage*x*1.3*0.5+ Damage*0

一般來說，以投資全球股市而言，大多是建議使用無貨幣避險的股市基金。債券部分，有些人會建議考慮本國貨幣避險的債券基金。但有提供新台幣避險的基金，選擇非常有限，且手續費等其他條件也並不是非常理想。 至於直接向銀行購買新台幣相關的遠期外匯交易或選擇權，對一般散戶來說困難重重。別的不說，光是常見的最低額度:一百萬美元，就不是人人都可以達到的。 如果你有「小額」的避險需求，比如十幾萬美元的曝險，且不介意引入部分股市風險的話，或許可以考慮一下這個想法: 台灣期貨交易所提供新台幣計價的臺灣證券交易所股價指數期貨。新加坡期貨交易所的FTSE台灣指數期貨與香港交易所的MSCI台灣指數期貨則是美元計價。小台一口約84萬NTD，摩台/富台約6.8萬/5.9萬USD。 假設你持有一些美元避險的債券基金，想把部分美元曝險換成新台幣曝險。可考慮 short 小台，long 摩台/富台。若美元下跌，摩台/富台的指數會上漲，彌補美元曝險部位的損失。 這個想法最大的缺點是小台/摩台/富台成分股其實不太一樣，會引入部分股市風險。另外，摩台/富台的獲利屬於海外所得，賺太多要課稅，不能用小台部位的損失抵稅。 舉例來說: 假設原本持有5.9萬USD，匯率28.5=168.15萬NTD。在富台1477點買進一口，在台指16841點 Short 2口小台。(2021/04/09價位) Scenario 1: 美元跌10%跌到25.65，台股沒漲跌 小台不變，富台漲到1641點。 Mark-to-market會有164*40=6560 USD被加到帳戶 => 現在手上65560 USD = 168.16萬 NTD Scenario 2: 匯率保持28.5，台股漲10% 小台變18525，富台變1625點 Mark-to-market 148*40=5920 USD被加到帳戶 2*1684*50=168400 NTD從帳戶扣除 => 現在手上64920 USD - 168400 NTD = 168.18萬 NTD Scenario 3: 匯率跌到25.65，台股漲10% 小台變18525，富台變1805.5點 Mark-to-market 328.5*40=13140 USD被加到帳戶 2*1684*50=168400 NTD從帳戶扣除 => 現在手上72140 USD - 168400 NTD