Daze

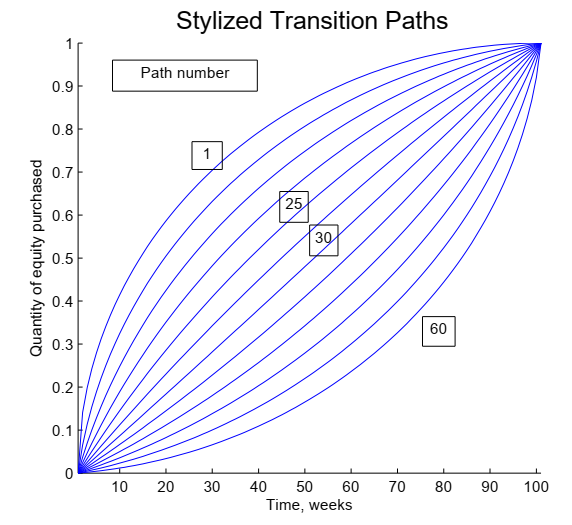
單筆投入的報酬期望值會勝過定期定額，許多文獻多有闡述。不過如果目標是"最小化後悔"的話，可能會有所不同。 Ordine, A. (2017) 是這樣定義後悔的:      後悔= 股票的購入價格 - 期間的最低價 這個定義下，買了以後下跌後悔，沒買結果漲上去也後悔，而且少賺跟多賠的後悔程度是相當的。總之，沒買到最低價就後悔。 舉例來說，你想要在1個月內購買100股ABC。期初股價50元，期間最低價40元，期末股價60元。如果在期初就買進100股。後悔 = 100*(50-40)=1000。如果期初買50股，期末買50股。後悔 = 50*(50-40) + 50*(60-40)=1500。 假設股票回報滿足對數常態分佈，Ordine指出最小化後悔期望值的投入方式是稍微concave的曲線，即早期投入速度較晚期稍快。以作者舉例的數字來說，是下左圖，標為25的曲線。(圖中的30是linear，即定期定股投入。)。作者也指出，設定的投入時間越長，最小化後悔的曲線會越concave，越偏向早期投入。 至於到底是"報酬期望值"比較重要，還是"最小化後悔"比較重要，就是個人選擇了。另外，作者衡量後悔的方式，也未必適用於其他人。 Reference: Ordine, A. (2017). Min-Regret Methods in Portfolio Transition. Available at SSRN 3006742.

所謂 定期定額( Dollar cost averaging) ，是指當投資人有大筆資金要投資時，不選擇 單筆投入( lump sum) ，而是選擇分成幾筆，按事先固定的時間投入 (註1) 。 要選擇定期定額 或是 單筆投入 是個歷久不衰的話題。雖然學術界三、四十年前似乎對此早有定論， 但定期定額這個想法在一般投資人間，仍然頗受歡迎 。 假設股票風險溢酬為正且股票回報滿足獨立同分布(Independent and identically distributed)，單筆投入早在多年前就已被證明回報率優於定期定額。然而，現實世界的經驗並不完全支持這些前提。 Brennan(2005)指出 (註2) ，假設股票回報存在相當程度的均值回歸(mean reversion)，則定期定額可能會勝過單筆投入。(Brennan衡量"勝過"的方式是基於utility function的一種變體型式 (註3) )。再者，他觀察到 相對於全市場， 對單一股票的定期定額更容易勝過同一股票的單筆投資。 至於單一股票是否較全市場有較高的均值回歸則沒有被探討。 如果一定要買個股的話，定期定額或許可行？至於理性投資人是否會選擇大舉投資個股，另當別論。Brennan在論文中也指出即使採用定期定額方式購買個股，其效用也低於投資全市場。 話說回來，股票市場均值回歸的程度是個實務問題，過去經驗只能提供對未來的部分預測，至於預測正確與否只能事後檢驗。另外，即使假設定期定額或許部分有效，最佳的期數與時間間隔也不見得能事先決定。 其他可能選擇定期定額的理由，可能包括： 衡量風險的方式並非基於波動與回報、 借款受限的投資人、 行為經濟學、 認知偏誤等等。 註1:除非假設投資人能用無風險利率無限制借貸，否則因為每個月薪水只有這麼多所以只能分次投入並不是典型的DCA vs lump sum問題 。 註2: Brennan的論文分別做了歷史資料回測與數值模擬， 兩者得到類似結論， 並沒有提供嚴格數學證明。 註3: 「確定的5%回報率」在效用上優於「平均5%，標準差16%的回報率」。 如果你在「確定的4.4%回報率」，與「平均5%，標準差16%的回報率」間沒有偏好， 則4.4%是你對「平均5%，標準差16%的回報率」的certainty equivalent。 Brennan比較的是DCA與lump s...