Daze

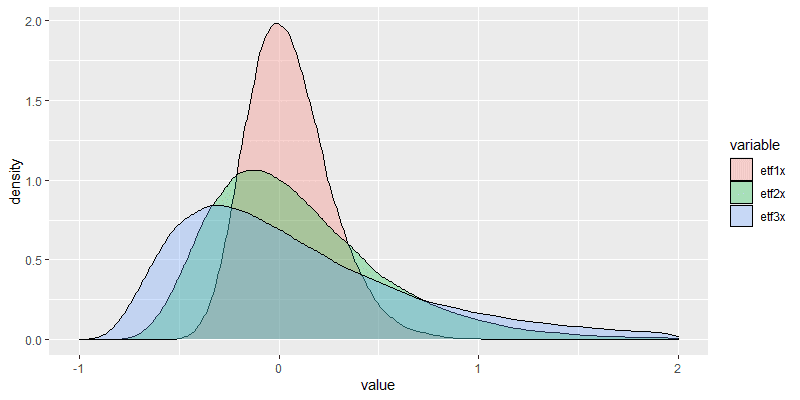
假設Daily return滿足normal distribution。 令Daily return=2bp，Daily SD= 125bp。 (每年約250交易日，約當年報酬率5%，年標準差20%) 生成100000筆250日的日回報率。 在不考慮ETF cost 的狀況下，250個交易日後，1x、2x、3xETF的回報率: 1xETF median 3.15%，mean 5.11%，SD 21.00% 2xETF median 2.33%，mean 10.48%，SD 45.44% 3xETF median -2.41%，mean 16.13%，SD 75.38% 加入cost (1xETF daily cost = 0, 2xETF daily cost=0.6bp, 3xETF daily cost=0.8bp，約當ER 1%，借貸成本 0.5%): 1xETF median 3.15%，mean 5.11%，SD 21.00% 2xETF median 0.81%，mean 8.84%，SD 44.77% 3xETF median -4.34%，mean 13.83%，SD 73.90% 不考慮cost，比較50%  1xETF + 50% 3xETF不再平衡 vs 100% 2xETF: 2xETF median 2.33%，mean 10.48%，SD 45.44% 50%  1xETF + 50% 3xETF不再平衡   median 0.37%， mean 10.62%，SD 47.85% 加入cost   (1xETF daily cost = 0, 2xETF daily cost=0.6bp, 3xETF daily cost=0.8bp)， 比較50%  1xETF + 50% 3xETF不再平衡 vs 100% 2xETF: 2xETF median 0.81%， mean 8.84%，SD 44.77% 50%  1xETF + 50% 3xETF不再平衡  median -0.59%，mean 9.47%，SD 47.11% Margin loan 1倍投入1xETF vs 2xETF (不考慮強制平倉): 註: 各張圖的value 大於2的部分被刻意切掉了，否則0附...

某甲想要貸款兩千萬買現值三千萬的房子，他對貸款會有那些期待? 他會希望利率越低越好。他不希望銀行可以隨時強迫他還貸款，或是房價下跌時要強迫補擔保品或強迫賣掉。他不希望借跟薪水不同的貨幣，以避免匯率風險。 類似地，某乙想要貸款買股票，他的期待也一樣。 a.低利率 b. non-callable c.與薪水相同貨幣。不幸的是，對於台灣投資人，這三點不太容易同時被滿足。也存在其他值得考慮的特性，比如: puttable，但相對沒有那麼重要。 具體有那些常見的借款工具呢? 台幣房貸 台幣信貸 美元融資 期貨 選擇權 台幣股票融資、美元信貸等等通常不太可行，但如果你有機會接觸到條件看似可行的選項的話，也不妨研究看看。 1.台幣房貸: 如果某乙的資產中已經有不動產了，以不動產做為擔保品，最容易得到能同時滿足三個條件的貸款。但現有資產中是否已有不動產，往往要看祖先有沒有遺留下來，沒有的話也沒辦法。 2.台幣信貸: 如果不能借房貸，台幣信貸通常能滿足條件b與條件c，至於條件a則要看個人的信用與收入狀態。另外，信貸通常無法借到兩千萬，常見的一個限制是月收入的22倍。 3.美元股票融資: 國外券商 Interactive broker 提供低利率的股票融資借款，前10萬美元目前年利率1.57%，借得更多利率還可以更低。在條件a來說還不錯，但條件b與條件c都不滿足。具體能借的金額根據帳戶內資產而定，portfolio margin甚至可以借到9倍以上。但借得倍數多，遇到margin call的風險也大。 4.期貨: 最有名的大概是CBOE交易所的e-mini/micro S&P 500(ES/MES)，目前隱含利率約1%。一口ES目前價值約190,000USD，保證金需求為11,000USD，槓桿開到滿，倍率高達17倍。一口MES目前價值約19,000USD。條件a來說甚至比美元股票融資更好，但條件b與條件c也都不滿足。另外ES每3個月要轉倉一次。其他可能的選擇比如EUREX交易所的歐元計價期貨，隱含利率甚至可能低於0，不過台灣人可能比較不熟悉。 5.美股選擇權: 常用的方法包括synthetic long與Deep-in-money call。 Synthetic long的特性頗類似期貨。Deep-in-money call則具有non-callable特性，滿足條件b。但S...

假設某甲有不錯的收入，不錯的工作穩定度，一千萬元台幣的存款。他有個聽起來還算普通的理想:「退休時有一棟在台北市的房子，還有一千萬元台幣定存。」。面對這個狀況，一般人會怎麼做?也許某甲會決定跟銀行借兩千萬貸款，買現值三千萬的房子，然後花三十年還貸款跟存款。這做法聽起來也還算普通。 假設某乙是某甲的同事，有類似的年齡、收入、工作穩定度與存款。某乙的理想是「退休時有相當數量的股票，還有一千萬元台幣定存。」。他會怎麼做? Lifecycle investing會建議某乙可能的話跟銀行借兩千萬貸款，買現值三千萬的股票，然後花三十年還貸款跟存款。 某甲也許一開始決定貸款兩千萬買房子，但研究細節之後，可能會發現貸不到、貸款利率太貴、還不起等等，最後決定妥協只買現值兩千萬的房子，或者乾脆暫時放棄買房。類似地，某乙在研究細節之後，也許會決定借少一點或乾脆不借，但這部分容後再談。基礎想法是如果某甲貸款買房是值得考慮的，則某乙貸款買股票也值得探討其可行性。 Lifecycle investing最基礎的想法就是這樣。如果你覺得這個想法有道理，那可以繼續探討細節的可行性。如果你覺得這完全是胡說八道，或許就只是Lifecycle investing並不適合你。就像某甲的做法聽起來很普通，但也許也有人反對。 進一步閱讀: Lifecycle investing-2-貸款的方式 Lifecycle investing-3-資產的配置 (還沒寫) <<Lifecycle Investing>> by  Ian Ayres & Barry Nalebuff

不太確定這個想法數學上是否robust(註1)，姑且聽聽看。 ====== Merton's solution 的 理想股債比 是  (1/η)*x/(s^2)，其中η是 相對風險趨避係數 ，x是股票溢酬，s是標準差。當借錢投資的時候，如果借款利率高於無風險利率，則槓桿部分的x會減少，但s不變。 If η=3, x=0.05, s=0.16，理想股債比是 65% 若借款利率是無風險利率+1%，理想股債比變成 52% 若借款利率是無風險利率+2%，理想股債比變成 39% 如果現有資產遠遠少於未來人力資本，則只要借款利差低於股票溢酬，仍然應該借好借滿。但如果現有資產已占人生總資產的相當比例，則隨著借款利率增加，理想股債比降低，達到理想股票配置的槓桿需求也會下降。再考慮到股票溢酬的不確定性、破產的disutility等等。某些狀況下也許持有100%股票配置會比較理想，使用槓桿並不會增加utility。 舉例來說，某人現有金融資產1000萬，未來人力資本折現1000萬。(姑且不討論應該如何折現才正確)。假設η=3, x=0.05, s=0.16，理想股債比是 65%，如果能以無風險利率借貸，應該借300萬達到1300萬股票部位。如果只能以無風險利率+1%借貸，x=(0.05-0.01)，理想股債比是 52%，應該借40萬達到1040萬股票部位。如果只能以無風險利率+2%借貸，x=(0.05-0.02)，理想股債比是 39%，與其借貸開槓桿，保持無槓桿的1000萬股票部位會更理想。 另外，匯率風險通常認為長期來說是中立的(註2)，但匯率風險會增加Variance，s^2的部分會增加，同樣會降低理想股債比。但作用的方式不太一樣。 假設USDTWD滿足常態分佈，標準差0.05。variance的上下界是 (0.16-0.05)^2 ~ (0.16+0.05)^2。(上下界應該可以再縮窄，但以我的數學能力有點困難。)。理想股債比要乘以 2.11~0.58。但似乎沒有很好的理由相信增加currency risk反而會減少變異度。或許在 1~0.58之間猜一個你覺得合理的數字。 原則上，Merton's portfolio problem在分配兩種資產時比較容易求解。在某些限制條件下，三種資產分配可以簡化成兩種資產分配問題。比如說，分配「股票」、「無風險利率債券」、「無...