Daze

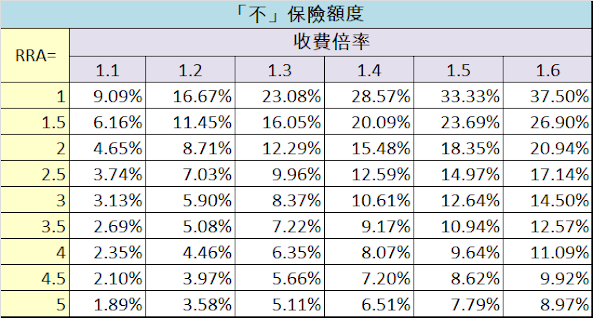
假設有一家保險公司能夠精準計算你的各項風險並承保。但是在精算出你的風險保費之後，要乘上一定的倍率收取保費。你應該保多少額度呢? 假設效用函數滿足Constant Relative Risk Aversion，且事件發生率不太大，理想的「不」保險額度約等於 1 - x^(-1/y)，其中 x 是收費倍率，y是 相對風險趨避係數(RRA) 。 (註1) 舉例來說，一個RRA=2的人，在倍率=1.3的狀況下，理想的「不」保險額度約等於12.29%。這個百分比是相對於總資產 (註2) 的額度。如果總資產有1000萬元，有一個事件的可能損害是300萬元，則應該為這個事件投保300萬-1000萬*12.29%=177.1萬的保險額度。事件可能損害如果低於122.9萬的話則應選擇完全不投保。 上面有提到，「事件發生率不太大的話」。理想的「不」保險額度會隨事件發生率提高而提高，隨可能損害降低而提高。不過以發生率10%來說，理想的「不」保險額度最多從12.29%上升到13.76%左右。 以汽車第三人責任險來說，如果能只保超額險的部分可能就比較理想了。可惜保險公司很少讓人稱心如意。 註1: 如果對計算過程有興趣，可參見 此 。 註2: 未來收入是否應折現計入總資產看個人觀點。我個人認為應該計入。

「風險自留」在保險上是個重要的觀念。對於低損害的事件，沒有保險的必要，可以自行承擔損失。那麼，什麼程度的損害才算夠低，而適合風險自留呢?在此試著透過 效用函數 的觀點提出一種解答。(假設效用函數滿足Constant Relative Risk Aversion) 假設有一家保險公司能夠精準計算你的各項風險並承保。但是保險公司畢竟不是慈善事業，在精算出你的風險保費之後，要乘上130%收取保費。哪些風險應該保險而哪些保險應該自留呢? 這個問題的答案，當然要看你對風險的趨避程度。越是不喜歡風險，即使較低的損害也可能有保險的必要。 上表的意義是，在130%保費下，如果相對風險趨避係數(RRA)為1，事件的損害等於總資產(註1)的45%，則當事件發生率小於7.28%時，保險的期望效用高於不保險的期望效用，應該保險。(註2) 但是，很容易注意到，上表有很多格子都是0。這些為0的格子，代表不管事件的發生率是多少，保險的期望效用都低於不保險的期望效用，應該不保險。 在130%保費下，如果你的RRA是1，總資產40%以下的損害應該不保險。RRA是2，總資產20%以下的損害應該不保險。RRA是3，總資產15%以下的損害應該不保險。 不過，上表是在完全保險與不保險之間做比較。如果允許只保一半呢? (理賠減半，保費也減半) 可以看到，為0的格子數減少了。 如果允許只保0.1倍風險的話，RRA=1在Damage= -0.25仍然有解。至於只保0.1倍風險是否實用另當別論。不過似乎找不到保險倍率能讓RRA=1在Damage= -0.2有解。(沒有解的Damage，RRA=1似乎是落在-0.23左右，RRA=2約-0.12，RRA=3約-0.08，RRA=4約-0.06。) 註1:我會建議將未來人力資本折現計入總資產。但也許有些人比較喜歡用現有總資產來計算。 註2:  如果想自行驗算表中數字，方程式是 ln( 1 + Damage)*x = ln(1 + Damage*x*1.3) ; if RRA=1 (1-(1+Damage)^(1-RRA))/(1-RRA)*x = (1 - (1+Damage*x*1.3)^(1-RRA))/(1-RRA) ; if RRA≠1 只保一半的方程式是 ln( 1 + Damage)*x = ln(1 + Damage*x*1.3*0.5+ Dama...

有些朋友們往往小孩剛出生就被推銷癌症險。其中一種推銷的話術是「五歲前是癌症高危險群」。然而，這句話在討論兒童醫學時是正確的，在討論保險時則有待商榷。 如果以兒童族群(0-14歲)做比較，如圖所示[1]，癌症最高發生率落在1歲以前，6~10歲間最低，之後又逐漸增加。但即便是0歲的癌症發生率，也才十萬分之25。 但若把年輕成人也納入比較，以 台灣癌症登記中心 的資料(2003～2007)，0-4歲的癌症發生率是十萬分之20.4/17.0 (男/女)，20-24歲的癌症發生率是十萬分之21.7/24.4，25-29歲的癌症發生率是十萬分之34.4/43.9。 0-4歲兒童的癌症發生率其實小於20-24歲成人。 不過，如果保險公司的定價方式是基於風險中立再加上固定比例費用，對風險趨避的客戶而言，發生機率越低的保險越可能有正的 utility。所以正確的說法或許是「你得癌症的機率很低，買癌症險最划算了。」。但如果定價方式是基於風險中立再加上固定金額費用就不是很理想。 Reference: 1. Hung, Giun-Yi et al. “Infant Cancer in Taiwan: Incidence and Trends (1995-2009).” PloS one vol. 10,6 e0130444. 25 Jun. 2015, doi:10.1371/journal.pone.0130444

相對風險趨避係數η 在 資產配置 的應用，數學上相對比較複雜，也許不是每位朋友都會認同。讓我們嘗試一些比較直觀的應用。 比如說，保險: 假設總資產1000萬，其中汽車價值100萬。預期一年內平安無事機率99%，發生車禍完全撞毀機率1%，是否該買要價x萬元的車體險?

市面上，癌症險也算是熱銷商品，但市售癌症險其實不符合大多數人的需求。 要談什麼樣的癌症險符合大多數人的需求，首先要談當前的癌症治療是怎麼樣，未來二十年的癌症治療趨勢又是如何。這些治療能花多少錢? 癌症治療目前的幾大模式: 1.手術 能開刀根治的，大多花不了太多錢，頂多幾十萬左右，而且健保可以cover大部分。 2.化療 大部分在健保給付的範圍內，某些新配方需自費。用到病人死掉為止，幾十萬到幾百萬。 3.標靶治療 過去20年的顯學，某些有健保給付，某些沒有。一個月十幾萬，可以延長病人數年壽命，但通常幾年後會出現抗藥性。用到病人死掉為止，幾百萬。 4.免疫療法/細胞療法 未來20年的顯學。目前還大多放在第三線之後，但有往第二線治療發展的趨勢。一個療程往往百萬起跳，甚至也有起手報價八百萬台幣的療程。如果沒有效，病人很快就會死掉，有效的話(目前來說，約20%左右有效)，有可能長期存活，已有存活十五年的案例。沒有效的話，可能要花個幾百萬；有效的話，要繼續使用，幾千萬都不見得夠。 支出很高但不會活很久的疾病，或會拖很久但支出相對不高的疾病，都不會是財務的最大威脅。免疫療法/細胞療法剛好符合支出很高，有效的話又可能讓癌症變成一個拖很久的病，Financial Toxicity 可以非常驚人。