風險自留的門檻 (Threshold of Risk Self-retention)

「風險自留」在保險上是個重要的觀念。對於低損害的事件，沒有保險的必要，可以自行承擔損失。那麼，什麼程度的損害才算夠低，而適合風險自留呢?在此試著透過效用函數的觀點提出一種解答。(假設效用函數滿足Constant Relative Risk Aversion)

假設有一家保險公司能夠精準計算你的各項風險並承保。但是保險公司畢竟不是慈善事業，在精算出你的風險保費之後，要乘上130%收取保費。哪些風險應該保險而哪些保險應該自留呢? 這個問題的答案，當然要看你對風險的趨避程度。越是不喜歡風險，即使較低的損害也可能有保險的必要。

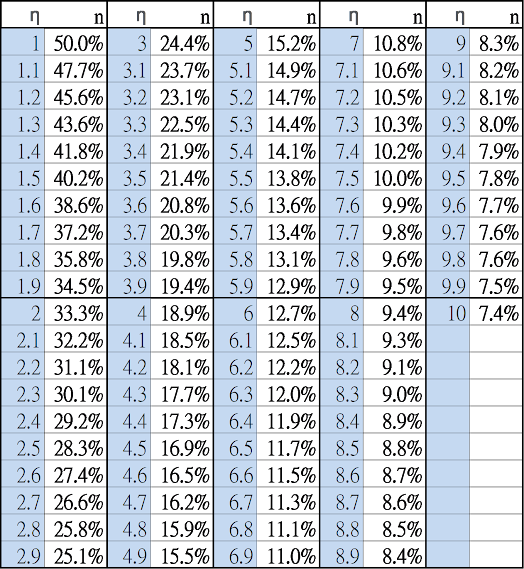
上表的意義是，在130%保費下，如果相對風險趨避係數(RRA)為1，事件的損害等於總資產(註1)的45%，則當事件發生率小於7.28%時，保險的期望效用高於不保險的期望效用，應該保險。(註2)

但是，很容易注意到，上表有很多格子都是0。這些為0的格子，代表不管事件的發生率是多少，保險的期望效用都低於不保險的期望效用，應該不保險。

在130%保費下，如果你的RRA是1，總資產40%以下的損害應該不保險。RRA是2，總資產20%以下的損害應該不保險。RRA是3，總資產15%以下的損害應該不保險。

不過，上表是在完全保險與不保險之間做比較。如果允許只保一半呢? (理賠減半，保費也減半)

可以看到，為0的格子數減少了。

如果允許只保0.1倍風險的話，RRA=1在Damage= -0.25仍然有解。至於只保0.1倍風險是否實用另當別論。不過似乎找不到保險倍率能讓RRA=1在Damage= -0.2有解。(沒有解的Damage，RRA=1似乎是落在-0.23左右，RRA=2約-0.12，RRA=3約-0.08，RRA=4約-0.06。)

註1:我會建議將未來人力資本折現計入總資產。但也許有些人比較喜歡用現有總資產來計算。

註2: 

如果想自行驗算表中數字，方程式是

ln( 1 + Damage)*x = ln(1 + Damage*x*1.3) ; if RRA=1

(1-(1+Damage)^(1-RRA))/(1-RRA)*x = (1 - (1+Damage*x*1.3)^(1-RRA))/(1-RRA) ; if RRA≠1

只保一半的方程式是

ln( 1 + Damage)*x = ln(1 + Damage*x*1.3*0.5+Damage*0.5)*x + ln(1 + Damage*x*1.3*0.5)*(1-x) ; if RRA=1

(1-(1+Damage)^(1-RRA))/(1-RRA)*x = (1 - (1+Damage*x*1.3*0.5+Damage*0.5)^(1-RRA))/(1-RRA)*x + (1 - (1+Damage*x*1.3*0.5)^(1-RRA))/(1-RRA)*(1-x) ; if RRA≠1