效用函數-3-應用:保險及其他 (utility function-3-insurance and others)

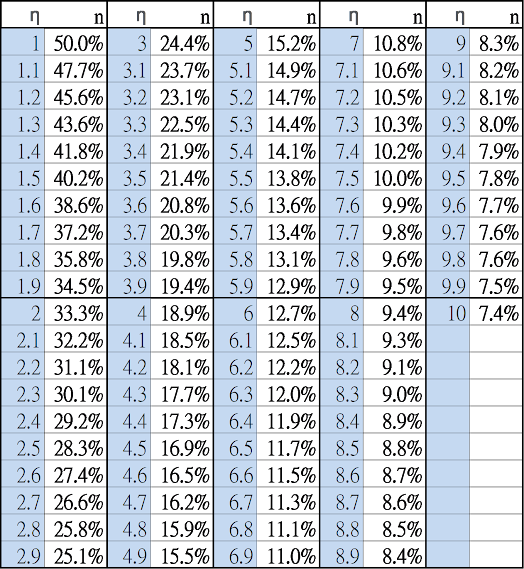
相對風險趨避係數η在資產配置的應用，數學上相對比較複雜，也許不是每位朋友都會認同。讓我們嘗試一些比較直觀的應用。

比如說，保險:

假設總資產1000萬，其中汽車價值100萬。預期一年內平安無事機率99%，發生車禍完全撞毀機率1%，是否該買要價x萬元的車體險?

If η=1，u(c)=ln(c)
不購買車體險的utility = ln(1000/1000)*0.99 + ln( (1000-100)/1000)*0.01

購買車體險的utility = ln((1000-x)/1000)*0.99 + ln((1000-x)/1000)*0.01
車體險要價小於1.05萬元時，購買車體險的utility就會大於不購買。

If η=3，u(c)=(c^(1-3)-1)/(1-3)
不購買車體險的utility = ((1000/1000)^(-2)-1)/(-2)*0.99 + (((1000-100)/1000)^(-2)-1)/(-2)*0.01
購買車體險的utility = (((1000-x)/1000)^(-2)-1)/(-2)*0.99 + (((1000-x)/1000)^(-2)-1)/(-2)*0.01

車體險要價小於1.17萬元時，購買車體險的utility就會大於不購買。

======

utility function也不只能用在財務規劃。

舉例來說，假設核四發生核災機率為x，核四商轉不發生核災可讓資產增加1%，發生核災會讓資產減少90%，是否該支持核四商轉?

If η=1，u(c)=ln(c)

(1-x)ln(1.01)+x*ln(0.1)==0, solve x

=> x=0.0043

如果核災機率大於0.43%，utility就變負的。

If η=3，u(c)=(c^(1-3)-1)/(1-3)

(1-x)*(1.01^(-2)-1)/(-2)+x*(0.1^(-2)-1)/(-2)==0, solve x

=> x=0.00020

如果核災機率大於0.02%，utility就變負的。

即使大家對於財產收益與損失的預期及核災的發生率相同，在不同的η之下，決定也可能是不同的。