效用函數-1-了解你自己 (Utility function-1-know thyself)
對大部分的人來說,賠一萬元的痛苦超過多賺一萬元的滿足。或者說,大部分的人是風險趨避(risk aversion)的。經濟學家用效用函數(Utility function)來描述這件事。然而,每個人的風險趨避程度不盡相同,而了解你自己在財務規劃上是很重要的。我們可以試著估計自己的風險趨避程度。
一個學術上常用的效用函數模型是Isoelastic utility function.
u(c)= (c^(1-η) - 1 )/(1-η) if η >= 0, η != 1
u(c) = ln(c) if η=1
舉例來說,若η=1,財產加倍(c=2)的滿足相當於財產減半(c=0.5)的痛苦。(c是指consumption,學術上要把消費對時間積分,把財產當作消費使用是種簡化)
Isoelastic utility function有其優點與缺點。缺點的部分日後再談,不妨先暫且接受此一模型並試著估計自己的相對風險趨避係數η (讀作ee-ta)。All models are wrong, but some are useful.
想像你今天中了10億威力彩。在領獎前,彩券公司說,你可以選擇是否玩一個遊戲。擲一個公正硬幣,如果是正面,獎金加倍,如果是背面,獎金減少 n%。n是多少,你才願意接受這個遊戲?
n=100,η=0,風險中立。
n=50,η=1。Log utility function。
n= 33.3,η=2。
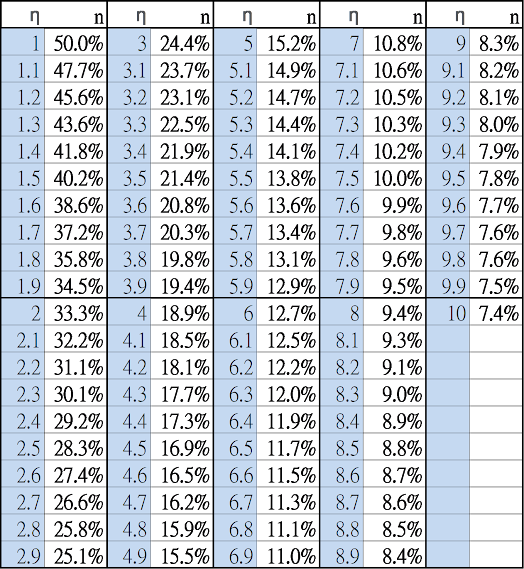
我們可以查閱下表得到η的近似值。舉例來說,如果你的n=25,則你的η就大約落在2.9跟3之間。得到自己的相對風險趨避係數η之後,後續可以嘗試一些實際應用。
2^(1-η) + ((100-n)/100)^(1-η)==2, solve η
留言
張貼留言