手續費低消、投資頻率與風險趨避 (Minimum commission, investing frequency and risk aversion)

複委託的手續費低消往往不低，受此影響，很多人會累積相當金額，待手續費超過低消之後才一次投資，但這不見得是最佳解。SweetLee在PTT的Foreign_Inv版的文章[心得] 複委託的手續費低消，探討了手續費低消與最佳化投資頻率的關係，得出 T = sqrt(2M/A/r) (手續費低消M,單位時間累積儲蓄A,單位時間內期望報酬率r,每筆的投資間隔是T)。

SweetLee得出的解是風險中立的。對風險中立的解來說，只要報酬率的平均值相同，報酬率的distribution是不影響解的，這點在求解上很方便。

那麼，風險規避的投資人的最佳解為何呢? 第一感可能會覺得，手續費是確定的開支,報酬是無保證的未來收益，風險規避的投資人應該拉長投資間隔，專注於減少手續費開支。不過真的如此嗎?

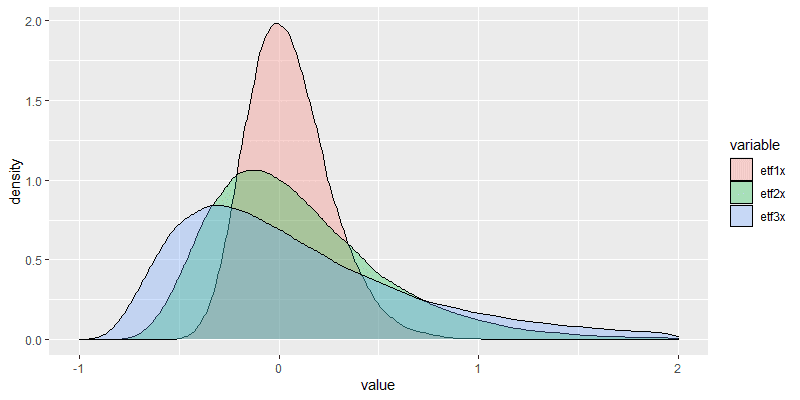
這類問題在數學上往往沒有顯然的解析解，而需要用數值方法求解。Baccarin, S., & Marazzina, D. (2013) 的定性觀察是，風險規避較高的投資人會較常付出交易費用，將portfolio調回理想比重。另一個定性觀察是，波動率越大，風險規避的投資人越傾向於再平衡。

當交易金額相對總資產不大時，風險中立的解跟風險規避的解的實際差距並不大。實務上直接套用SweetLee的解，大概也沒有太大的問題。在此只是提出一個看似反直覺的定性觀察，跟各位分享。


Reference: 
Baccarin, S., & Marazzina, D. (2013). Optimal impulse control of a portfolio with a fixed transaction cost. Central European Journal of Operations Research, 22(2), 355–372. doi:10.1007/s10100-013-0304-9 

留言

張貼留言

這個網誌中的熱門文章

槓桿ETF的蒙地卡羅模擬 (Leveraged ETF Monte Carlo)

圖片
假設Daily return滿足normal distribution。 令Daily return=2bp，Daily SD= 125bp。 (每年約250交易日，約當年報酬率5%，年標準差20%) 生成100000筆250日的日回報率。 在不考慮ETF cost 的狀況下，250個交易日後，1x、2x、3xETF的回報率: 1xETF median 3.15%，mean 5.11%，SD 21.00% 2xETF median 2.33%，mean 10.48%，SD 45.44% 3xETF median -2.41%，mean 16.13%，SD 75.38% 加入cost (1xETF daily cost = 0, 2xETF daily cost=0.6bp, 3xETF daily cost=0.8bp，約當ER 1%，借貸成本 0.5%): 1xETF median 3.15%，mean 5.11%，SD 21.00% 2xETF median 0.81%，mean 8.84%，SD 44.77% 3xETF median -4.34%，mean 13.83%，SD 73.90% 不考慮cost，比較50%  1xETF + 50% 3xETF不再平衡 vs 100% 2xETF: 2xETF median 2.33%，mean 10.48%，SD 45.44% 50%  1xETF + 50% 3xETF不再平衡   median 0.37%， mean 10.62%，SD 47.85% 加入cost   (1xETF daily cost = 0, 2xETF daily cost=0.6bp, 3xETF daily cost=0.8bp)， 比較50%  1xETF + 50% 3xETF不再平衡 vs 100% 2xETF: 2xETF median 0.81%， mean 8.84%，SD 44.77% 50%  1xETF + 50% 3xETF不再平衡  median -0.59%，mean 9.47%，SD 47.11% Margin loan 1倍投入1xETF vs 2xETF (不考慮強制平倉): 註: 各張圖的value 大於2的部分被刻意切掉了，否則0附近太擠了 註2: R code 註3: If considering
閱讀完整內容

Lifecycle investing-2-貸款的方式 (leverage choices)

某甲想要貸款兩千萬買現值三千萬的房子，他對貸款會有那些期待? 他會希望利率越低越好。他不希望銀行可以隨時強迫他還貸款，或是房價下跌時要強迫補擔保品或強迫賣掉。他不希望借跟薪水不同的貨幣，以避免匯率風險。 類似地，某乙想要貸款買股票，他的期待也一樣。 a.低利率 b. non-callable c.與薪水相同貨幣。不幸的是，對於台灣投資人，這三點不太容易同時被滿足。也存在其他值得考慮的特性，比如: puttable，但相對沒有那麼重要。 具體有那些常見的借款工具呢? 台幣房貸 台幣信貸 美元融資 期貨 選擇權 台幣股票融資、美元信貸等等通常不太可行，但如果你有機會接觸到條件看似可行的選項的話，也不妨研究看看。 1.台幣房貸: 如果某乙的資產中已經有不動產了，以不動產做為擔保品，最容易得到能同時滿足三個條件的貸款。但現有資產中是否已有不動產，往往要看祖先有沒有遺留下來，沒有的話也沒辦法。 2.台幣信貸: 如果不能借房貸，台幣信貸通常能滿足條件b與條件c，至於條件a則要看個人的信用與收入狀態。另外，信貸通常無法借到兩千萬，常見的一個限制是月收入的22倍。 3.美元股票融資: 國外券商 Interactive broker 提供低利率的股票融資借款，前10萬美元目前年利率1.57%，借得更多利率還可以更低。在條件a來說還不錯，但條件b與條件c都不滿足。具體能借的金額根據帳戶內資產而定，portfolio margin甚至可以借到9倍以上。但借得倍數多，遇到margin call的風險也大。 4.期貨: 最有名的大概是CBOE交易所的e-mini/micro S&P 500(ES/MES)，目前隱含利率約1%。一口ES目前價值約190,000USD，保證金需求為11,000USD，槓桿開到滿，倍率高達17倍。一口MES目前價值約19,000USD。條件a來說甚至比美元股票融資更好，但條件b與條件c也都不滿足。另外ES每3個月要轉倉一次。其他可能的選擇比如EUREX交易所的歐元計價期貨，隱含利率甚至可能低於0，不過台灣人可能比較不熟悉。 5.美股選擇權: 常用的方法包括synthetic long與Deep-in-money call。 Synthetic long的特性頗類似期貨。Deep-in-money call則具有non-callable特性，滿足條件b。但S
閱讀完整內容